nbsphinx

nbsphinx is a Sphinx extension that provides a source parser for *.ipynb files.

• Documentation: https://nbsphinx.readthedocs.io/

• Source Code: https://github.com/spatialaudio/nbsphinx

Install

pip install nbsphinx

Then, add the extension to your conf.py:

conf.py

extensions = [
    # ...
    "nbsphinx",
]

Examples

Here are some examples to show how nbsphinx rendering ipynb files.

Code, Output, Streams

An empty code cell:

Two empty lines:

Leading/trailing empty lines:

# 2 empty lines before, 1 after

A simple output:

6 * 7

42

The standard output stream:

print("Hello, world!")

Hello, world!

Normal output + standard output

print("Hello, world!")
6 * 7

Hello, world!

42

The standard error stream is highlighted and displayed just below the code cell. The standard output stream comes afterwards (with no special highlighting). Finally, the “normal” output is displayed.

import sys

print("I'll appear on the standard error stream", file=sys.stderr)
print("I'll appear on the standard output stream")
"I'm the 'normal' output"

I'll appear on the standard output stream

I'll appear on the standard error stream

"I'm the 'normal' output"

Note

Using the IPython kernel, the order is actually mixed up, see https://github.com/ipython/ipykernel/issues/280.

Math

from IPython.display import Math

eq = Math(r"\int\limits_{-\infty}^\infty f(x) \delta(x - x_0) dx = f(x_0)")
eq

$\displaystyle \int\limits_{-\infty}^\infty f(x) \delta(x - x_0) dx = f(x_0)$

display(eq)

$\displaystyle \int\limits_{-\infty}^\infty f(x) \delta(x - x_0) dx = f(x_0)$

from IPython.display import Latex

Latex(r"This is a \LaTeX{} equation: $a^2 + b^2 = c^2$")

This is a \LaTeX{} equation: $a^2 + b^2 = c^2$

%%latex
\begin{equation}
\int\limits_{-\infty}^\infty f(x) \delta(x - x_0) dx = f(x_0)
\end{equation}

\begin{equation} \int\limits_{-\infty}^\infty f(x) \delta(x - x_0) dx = f(x_0) \end{equation}

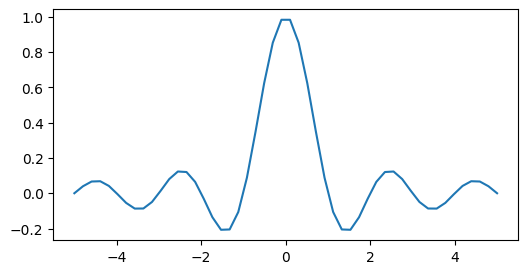
matplotlib

import matplotlib.pyplot as plt
import numpy as np

fig, ax = plt.subplots(figsize=[6, 3])
x = np.linspace(-5, 5, 50)
ax.plot(x, np.sinc(x));

YouTube Videos

from IPython.display import YouTubeVideo

YouTubeVideo("9_OIs49m56E")

Tables

import pandas as pd

data = [[1, 2], [3, 4]]
pd.DataFrame(data, columns=["Foo", "Bar"])

	Foo	Bar
0	1	2
1	3	4

ANSI Colors

The standard output and standard error streams may contain ANSI escape sequences to change the text and background colors.

print("BEWARE: \x1b[1;33;41mugly colors\x1b[m!", file=sys.stderr)
print("AB\x1b[43mCD\x1b[35mEF\x1b[1mGH\x1b[4mIJ\x1b[7mKL\x1b[49mMN\x1b[39mOP\x1b[22mQR\x1b[24mST\x1b[27mUV")

ABCDEFGHIJKLMNOPQRSTUV

BEWARE: ugly colors!

text = " XYZ "
formatstring = "\x1b[{}m" + text + "\x1b[m"

print(" " * 6 + " " * len(text) + "".join("{:^{}}".format(bg, len(text)) for bg in range(40, 48)))
for fg in range(30, 38):
    for bold in False, True:
        fg_code = ("1;" if bold else "") + str(fg)
        print(
            " {:>4} ".format(fg_code)
            + formatstring.format(fg_code)
            + "".join(formatstring.format(fg_code + ";" + str(bg)) for bg in range(40, 48))
        )

            40   41   42   43   44   45   46   47
   30  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ 
 1;30  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ 
   31  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ 
 1;31  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ 
   32  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ 
 1;32  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ 
   33  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ 
 1;33  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ 
   34  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ 
 1;34  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ 
   35  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ 
 1;35  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ 
   36  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ 
 1;36  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ 
   37  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ 
 1;37  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ  XYZ 

formatstring = "\x1b[38;5;{0};48;5;{0}mX\x1b[1mX\x1b[m"

print("  + " + "".join("{:2}".format(i) for i in range(36)))
print("  0 " + "".join(formatstring.format(i) for i in range(16)))
for i in range(7):
    i = i * 36 + 16
    print("{:3} ".format(i) + "".join(formatstring.format(i + j) for j in range(36) if i + j < 256))

  +  0 1 2 3 4 5 6 7 8 91011121314151617181920212223242526272829303132333435
  0 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
 16 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
 52 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
 88 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
124 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
160 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
196 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
232 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

start = 255, 0, 0
end = 0, 0, 255
length = 79
out = []

for i in range(length):
    rgb = [start[c] + int(i * (end[c] - start[c]) / length) for c in range(3)]
    out.append("\x1b[38;2;{rgb[2]};{rgb[1]};{rgb[0]};48;2;{rgb[0]};{rgb[1]};{rgb[2]}mX\x1b[m".format(rgb=rgb))
print("".join(out))

XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

Hint

This documentation itself is written in .ipynb. To view the source code, click the Edit this page link on the right sidebar.